What is the slope of a line that is perpendicular to y = 1/8x- 9?
Graphs
36 Employ the Gradient–Intercept Course of an Equation of a Line
Learning Objectives
By the end of this section, you will be able to:
- Recognize the relation between the graph and the slope–intercept form of an equation of a line
- Identify the slope and y-intercept form of an equation of a line
- Graph a line using its slope and intercept
- Choose the most convenient method to graph a line
- Graph and translate applications of slope–intercept
- Utilize slopes to identify parallel lines
- Use slopes to identify perpendicular lines
Recognize the Relation Between the Graph and the Gradient–Intercept Form of an Equation of a Line
We have graphed linear equations by plotting points, using intercepts, recognizing horizontal and vertical lines, and using the point–slope method. One time we see how an equation in slope–intercept form and its graph are related, we'll have ane more method we can use to graph lines.
In Graph Linear Equations in Two Variables, we graphed the line of the equation ![]() by plotting points. See (Figure). Permit'southward find the gradient of this line.
by plotting points. See (Figure). Permit'southward find the gradient of this line.
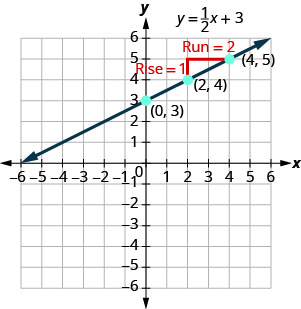
The cherry-red lines bear witness us the rise is ane and the run is 2. Substituting into the gradient formula:
![]()
What is the y-intercept of the line? The y-intercept is where the line crosses the y-axis, then y-intercept is ![]() . The equation of this line is:
. The equation of this line is:
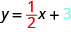
Detect, the line has:

When a linear equation is solved for ![]() , the coefficient of the
, the coefficient of the ![]() term is the slope and the abiding term is the y-coordinate of the y-intercept. We say that the equation
term is the slope and the abiding term is the y-coordinate of the y-intercept. We say that the equation ![]() is in slope–intercept class.
is in slope–intercept class.
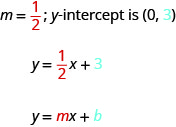
Slope-Intercept Form of an Equation of a Line
The gradient–intercept course of an equation of a line with slope ![]() and y-intercept,
and y-intercept, ![]() is,
is,
![]()
Sometimes the slope–intercept course is called the "y-form."
Use the graph to find the slope and y-intercept of the line, ![]() .
.
Compare these values to the equation![]() .
.
Use the graph to find the slope and y-intercept of the line ![]() . Compare these values to the equation
. Compare these values to the equation ![]() .
.
slope ![]() and y-intercept
and y-intercept ![]()
Use the graph to discover the gradient and y-intercept of the line ![]() . Compare these values to the equation
. Compare these values to the equation ![]() .
.
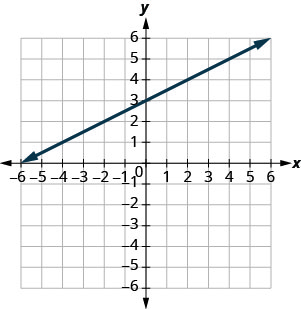
slope ![]() and y-intercept
and y-intercept ![]()
Identify the Slope and y-Intercept From an Equation of a Line
In Understand Gradient of a Line, we graphed a line using the slope and a point. When we are given an equation in slope–intercept course, we tin can use the y-intercept as the signal, and then count out the slope from there. Let'south practise finding the values of the gradient and y-intercept from the equation of a line.
Place the slope and y-intercept of the line with equation ![]() .
.
Solution
Nosotros compare our equation to the slope–intercept course of the equation.
 | |
| Write the equation of the line. | 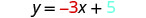 |
| Identify the slope. |  |
| Identify the y-intercept. | 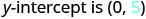 |
Identify the slope and y-intercept of the line ![]() .
.
![]()
Place the slope and y-intercept of the line ![]() .
.
![]()
When an equation of a line is not given in gradient–intercept class, our first step will be to solve the equation for ![]() .
.
Place the slope and y-intercept of the line with equation ![]() .
.
Place the slope and y-intercept of the line ![]() .
.
![]()
Identify the slope and y-intercept of the line ![]() .
.
![]()
Graph a Line Using its Slope and Intercept
Now that we know how to observe the slope and y-intercept of a line from its equation, we can graph the line by plotting the y-intercept and then using the gradient to find another point.
How to Graph a Line Using its Slope and Intercept
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
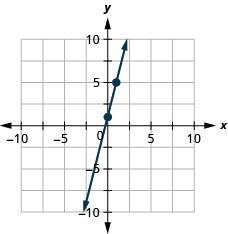
Graph the line of the equation ![]() using its gradient and y-intercept.
using its gradient and y-intercept.
Graph a line using its slope and y-intercept.
- Find the slope-intercept course of the equation of the line.
- Identify the slope and y-intercept.
- Plot the y-intercept.
- Use the slope formula
 to identify the rise and the run.
to identify the rise and the run. - Starting at the y-intercept, count out the rise and run to mark the 2nd point.
- Connect the points with a line.
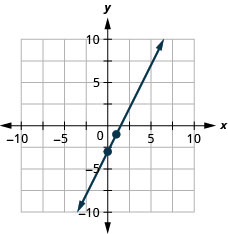
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its gradient and y-intercept.
using its gradient and y-intercept.
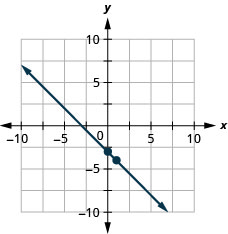
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its gradient and y-intercept.
using its gradient and y-intercept.
Graph the line of the equation ![]() using its gradient and y-intercept.
using its gradient and y-intercept.
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
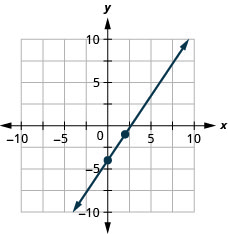
We have used a filigree with ![]() and
and ![]() both going from well-nigh
both going from well-nigh ![]() to 10 for all the equations we've graphed and then far. Not all linear equations can be graphed on this small grid. Often, especially in applications with real-world data, we'll need to extend the axes to bigger positive or smaller negative numbers.
to 10 for all the equations we've graphed and then far. Not all linear equations can be graphed on this small grid. Often, especially in applications with real-world data, we'll need to extend the axes to bigger positive or smaller negative numbers.
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
Graph the line of the equation ![]() using its gradient and y-intercept.
using its gradient and y-intercept.
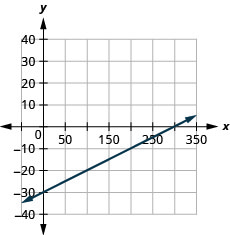
Graph the line of the equation ![]() using its slope and y-intercept.
using its slope and y-intercept.
At present that we have graphed lines by using the gradient and y-intercept, let's summarize all the methods we have used to graph lines. See (Effigy).

Cull the Most User-friendly Method to Graph a Line
At present that we accept seen several methods we tin can employ to graph lines, how do we know which method to employ for a given equation?
While we could plot points, utilise the slope–intercept grade, or notice the intercepts for any equation, if we recognize the most convenient way to graph a sure blazon of equation, our piece of work will be easier. Generally, plotting points is not the most efficient way to graph a line. We saw meliorate methods in sections iv.3, 4.4, and earlier in this section. Let's look for some patterns to help determine the most convenient method to graph a line.
Here are half dozen equations we graphed in this chapter, and the method we used to graph each of them.
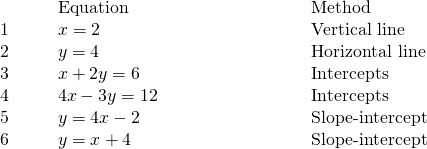
Equations #1 and #2 each have only one variable. Recall, in equations of this form the value of that one variable is abiding; it does non depend on the value of the other variable. Equations of this form take graphs that are vertical or horizontal lines.
In equations #iii and #4, both ![]() and
and ![]() are on the same side of the equation. These two equations are of the form
are on the same side of the equation. These two equations are of the form ![]() . We substituted
. We substituted ![]() to find the ten-intercept and
to find the ten-intercept and ![]() to detect the y-intercept, and then establish a 3rd point by choosing another value for
to detect the y-intercept, and then establish a 3rd point by choosing another value for ![]() or
or ![]() .
.
Equations #5 and #vi are written in slope–intercept form. Subsequently identifying the gradient and y-intercept from the equation nosotros used them to graph the line.
This leads to the following strategy.
Strategy for Choosing the Most User-friendly Method to Graph a Line
Consider the form of the equation.
Decide the virtually convenient method to graph each line.
ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]() ⓓ
ⓓ ![]() .
.
Decide the most convenient method to graph each line: ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]() ⓓ
ⓓ ![]() .
.
ⓐ interceptsⓑ horizontal lineⓒ gradient–interceptⓓ vertical line
Determine the almost convenient method to graph each line: ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]() ⓓ
ⓓ ![]() .
.
ⓐ vertical lineⓑ gradient–interceptⓒ horizontal lineⓓ intercepts
Graph and Interpret Applications of Gradient–Intercept
Many real-earth applications are modeled by linear equations. Nosotros will have a look at a few applications here so you can see how equations written in slope–intercept form relate to real-world situations.
Usually when a linear equation models a existent-world situation, different messages are used for the variables, instead of x and y. The variable names remind us of what quantities are beingness measured.
The equation ![]() is used to convert temperatures,
is used to convert temperatures, ![]() , on the Celsius scale to temperatures,
, on the Celsius scale to temperatures, ![]() , on the Fahrenheit scale.
, on the Fahrenheit scale.
ⓐ Find the Fahrenheit temperature for a Celsius temperature of 0.
ⓑ Observe the Fahrenheit temperature for a Celsius temperature of twenty.
ⓒ Interpret the slope and F-intercept of the equation.
ⓓ Graph the equation.
Solution
| ⓐ Find the Fahrenheit temperature for a Celsius temperature of 0. Discover Simplify. | 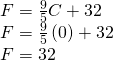 |
| ⓑ Find the Fahrenheit temperature for a Celsius temperature of twenty. Observe Simplify. Simplify. | 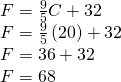 |
ⓒ Translate the slope and F-intercept of the equation.
Even though this equation uses ![]() and
and ![]() , information technology is notwithstanding in slope–intercept form.
, information technology is notwithstanding in slope–intercept form.
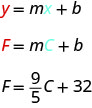
The slope, ![]() , ways that the temperature Fahrenheit (F) increases 9 degrees when the temperature Celsius (C) increases 5 degrees.
, ways that the temperature Fahrenheit (F) increases 9 degrees when the temperature Celsius (C) increases 5 degrees.
The F-intercept means that when the temperature is ![]() on the Celsius calibration, it is
on the Celsius calibration, it is ![]() on the Fahrenheit scale.
on the Fahrenheit scale.
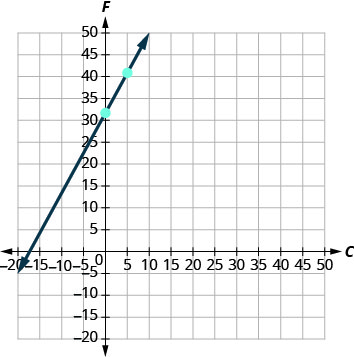
ⓓ Graph the equation.
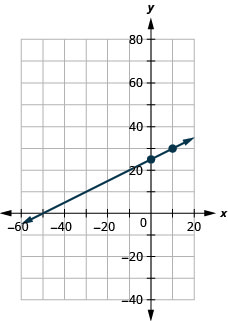
Nosotros'll demand to use a larger calibration than our usual. Starting time at the F-intercept ![]() and so count out the rise of ix and the run of 5 to become a second signal. See (Figure).
and so count out the rise of ix and the run of 5 to become a second signal. See (Figure).
The equation ![]() is used to estimate a adult female's height in inches, h, based on her shoe size, s.
is used to estimate a adult female's height in inches, h, based on her shoe size, s.
ⓐ Estimate the peak of a child who wears women's shoe size 0.
ⓑ Estimate the height of a woman with shoe size viii.
ⓒ Translate the gradient and h-intercept of the equation.
ⓓ Graph the equation.
- ⓐ fifty inches
- ⓑ 66 inches
- ⓒ The slope, 2, means that the meridian, h, increases past 2 inches when the shoe size, due south, increases past 1. The h-intercept means that when the shoe size is 0, the meridian is 50 inches.
- ⓓ
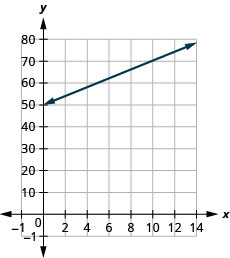
The equation ![]() is used to estimate the temperature in degrees Fahrenheit, T, based on the number of cricket chirps, due north, in i infinitesimal.
is used to estimate the temperature in degrees Fahrenheit, T, based on the number of cricket chirps, due north, in i infinitesimal.
ⓐ Gauge the temperature when there are no chirps.
ⓑ Judge the temperature when the number of chirps in one minute is 100.
ⓒ Interpret the gradient and T-intercept of the equation.
ⓓ Graph the equation.
The cost of running some types business organisation has two components—a fixed price and a variable cost. The fixed toll is always the same regardless of how many units are produced. This is the price of rent, insurance, equipment, advertising, and other items that must be paid regularly. The variable cost depends on the number of units produced. It is for the material and labor needed to produce each item.
Stella has a home business organisation selling gourmet pizzas. The equation ![]() models the relation between her weekly cost, C, in dollars and the number of pizzas, p, that she sells.
models the relation between her weekly cost, C, in dollars and the number of pizzas, p, that she sells.
ⓐ Find Stella'due south price for a week when she sells no pizzas.
ⓑ Observe the cost for a week when she sells 15 pizzas.
ⓒ Interpret the slope and C-intercept of the equation.
ⓓ Graph the equation.
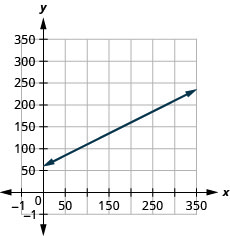
Sam drives a delivery van. The equation ![]() models the relation between his weekly cost, C, in dollars and the number of miles, m, that he drives.
models the relation between his weekly cost, C, in dollars and the number of miles, m, that he drives.
ⓐ Find Sam'south cost for a week when he drives 0 miles.
ⓑ Find the toll for a week when he drives 250 miles.
ⓒ Interpret the slope and C-intercept of the equation.
ⓓ Graph the equation.
- ⓐ ?threescore
- ⓑ ?185
- ⓒ The gradient, 0.5, means that the weekly cost, C, increases past ?0.fifty when the number of miles driven, n, increases by 1. The C-intercept ways that when the number of miles driven is 0, the weekly cost is ?60
- ⓓ
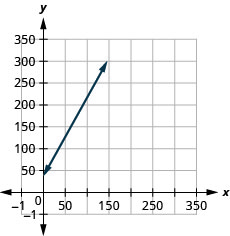
Loreen has a calligraphy business. The equation ![]() models the relation between her weekly toll, C, in dollars and the number of wedding invitations, n, that she writes.
models the relation between her weekly toll, C, in dollars and the number of wedding invitations, n, that she writes.
ⓐ Find Loreen's toll for a week when she writes no invitations.
ⓑ Find the cost for a week when she writes 75 invitations.
ⓒ Interpret the slope and C-intercept of the equation.
ⓓ Graph the equation.
- ⓐ ?35
- ⓑ ?170
- ⓒ The slope, one.8, means that the weekly cost, C, increases by ?1.80 when the number of invitations, n, increases past 1.80.
The C-intercept ways that when the number of invitations is 0, the weekly cost is ?35.; - ⓓ
Use Slopes to Identify Parallel Lines
The slope of a line indicates how steep the line is and whether it rises or falls every bit we read it from left to right. 2 lines that have the same slope are called parallel lines. Parallel lines never intersect.

We say this more than formally in terms of the rectangular coordinate organization. 2 lines that have the same slope and different y-intercepts are called parallel lines. See (Effigy).
Verify that both lines have the aforementioned slope, ![]() , and different y-intercepts.
, and different y-intercepts.
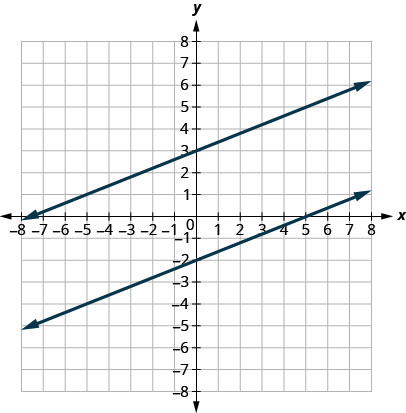
What nigh vertical lines? The gradient of a vertical line is undefined, then vertical lines don't fit in the definition higher up. We say that vertical lines that take different 10-intercepts are parallel. Come across (Figure).
Vertical lines with diferent x-intercepts are parallel.
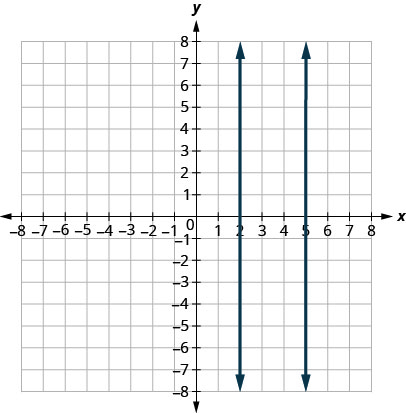
Parallel Lines
Parallel lines are lines in the aforementioned aeroplane that do not intersect.
Permit'south graph the equations ![]() and
and ![]() on the same filigree. The offset equation is already in slope–intercept class:
on the same filigree. The offset equation is already in slope–intercept class: ![]() . Nosotros solve the second equation for
. Nosotros solve the second equation for ![]() :
:
![]()
Graph the lines.
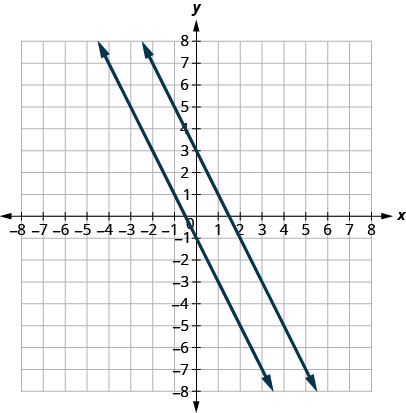
Find the lines look parallel. What is the slope of each line? What is the y-intercept of each line?

The slopes of the lines are the same and the y-intercept of each line is different. So nosotros know these lines are parallel.
Since parallel lines have the same gradient and different y-intercepts, we can now just look at the slope–intercept grade of the equations of lines and decide if the lines are parallel.
Utilise slopes and y-intercepts to determine if the lines ![]() and
and ![]() are parallel.
are parallel.
Utilise slopes and y-intercepts to determine if the lines ![]() are parallel.
are parallel.
parallel
Utilize slopes and y-intercepts to decide if the lines ![]() are parallel.
are parallel.
parallel
Utilize slopes and y-intercepts to determine if the lines ![]() and
and ![]() are parallel.
are parallel.
Use slopes and y-intercepts to determine if the lines ![]() are parallel.
are parallel.
parallel
Use slopes and y-intercepts to determine if the lines ![]() are parallel.
are parallel.
parallel
Use slopes and y-intercepts to determine if the lines ![]() and
and ![]() are parallel.
are parallel.
Solution
![]()
Since at that place is no![]() , the equations cannot exist put in slope–intercept form. But we recognize them as equations of vertical lines. Their x-intercepts are
, the equations cannot exist put in slope–intercept form. But we recognize them as equations of vertical lines. Their x-intercepts are ![]() and
and ![]() . Since their 10-intercepts are different, the vertical lines are parallel.
. Since their 10-intercepts are different, the vertical lines are parallel.
Apply slopes and y-intercepts to determine if the lines ![]() and
and ![]() are parallel.
are parallel.
parallel
Use slopes and y-intercepts to determine if the lines ![]() and
and ![]() are parallel.
are parallel.
parallel
Use slopes and y-intercepts to determine if the lines ![]() and
and ![]() are parallel. You may want to graph these lines, as well, to run across what they expect similar.
are parallel. You may want to graph these lines, as well, to run across what they expect similar.
Use slopes and y-intercepts to decide if the lines ![]() and
and ![]() are parallel.
are parallel.
not parallel; same line
Use slopes and y-intercepts to decide if the lines ![]() and
and ![]() are parallel.
are parallel.
not parallel; same line
Utilise Slopes to Identify Perpendicular Lines
Allow's look at the lines whose equations are ![]() and
and ![]() , shown in (Figure).
, shown in (Figure).
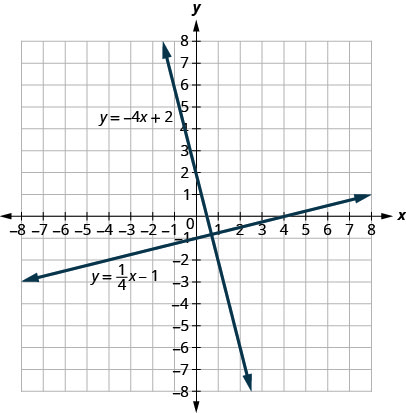
These lines lie in the same airplane and intersect in right angles. We telephone call these lines perpendicular.
What do you notice near the slopes of these 2 lines? Equally nosotros read from left to correct, the line ![]() rises, and so its slope is positive. The line
rises, and so its slope is positive. The line![]() drops from left to correct, and so information technology has a negative gradient. Does it make sense to y'all that the slopes of two perpendicular lines will have opposite signs?
drops from left to correct, and so information technology has a negative gradient. Does it make sense to y'all that the slopes of two perpendicular lines will have opposite signs?
If we look at the slope of the first line, ![]() , and the slope of the second line,
, and the slope of the second line, ![]() , we can come across that they are negative reciprocals of each other. If nosotros multiply them, their production is
, we can come across that they are negative reciprocals of each other. If nosotros multiply them, their production is ![]()
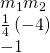
This is e'er true for perpendicular lines and leads us to this definition.
Perpendicular Lines
Perpendicular lines are lines in the same plane that course a right bending.
If ![]() are the slopes of two perpendicular lines, and then:
are the slopes of two perpendicular lines, and then:
![]()
Vertical lines and horizontal lines are e'er perpendicular to each other.
We were able to look at the slope–intercept class of linear equations and determine whether or non the lines were parallel. We can do the same thing for perpendicular lines.
Nosotros find the slope–intercept form of the equation, and then see if the slopes are negative reciprocals. If the product of the slopes is ![]() , the lines are perpendicular. Perpendicular lines may have the same y-intercepts.
, the lines are perpendicular. Perpendicular lines may have the same y-intercepts.
Use slopes to determine if the lines, ![]() and
and ![]() are perpendicular.
are perpendicular.
Solution
| The kickoff equation is already in slope-intercept form. | | |
| Solve the 2nd equation for | 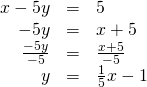 | |
| Identify the slope of each line. | 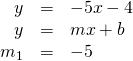 | 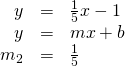 |
The slopes are negative reciprocals of each other, so the lines are perpendicular. We check by multiplying the slopes,
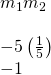
Use slopes to make up one's mind if the lines ![]() and
and ![]() are perpendicular.
are perpendicular.
perpendicular
Utilize slopes to determine if the lines ![]() and
and ![]() are perpendicular.
are perpendicular.
perpendicular
Use slopes to determine if the lines, ![]() and
and ![]() are perpendicular.
are perpendicular.
Utilize slopes to determine if the lines ![]() and
and ![]() are perpendicular.
are perpendicular.
non perpendicular
Utilize slopes to determine if the lines ![]() and
and ![]() are perpendicular.
are perpendicular.
non perpendicular
Key Concepts
Practice Makes Perfect
Recognize the Relation Betwixt the Graph and the Slope–Intercept Form of an Equation of a Line
In the post-obit exercises, use the graph to notice the slope and y-intercept of each line. Compare the values to the equation ![]() .
.
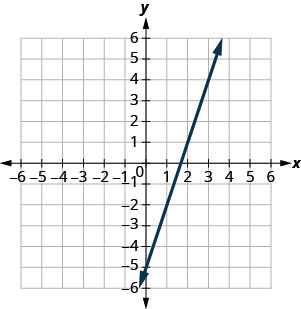
![]()
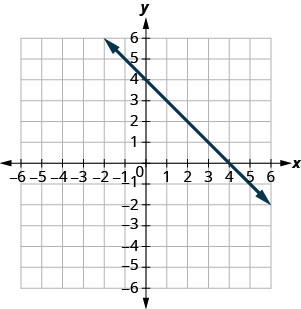
![]()
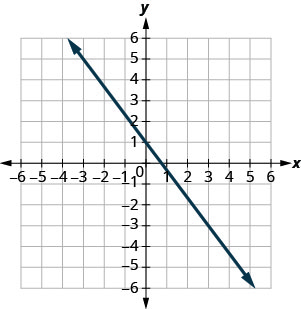
![]()
Identify the Gradient and y-Intercept From an Equation of a Line
In the following exercises, identify the slope and y-intercept of each line.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Graph a Line Using Its Slope and Intercept
In the following exercises, graph the line of each equation using its gradient and y-intercept.
![]()
![]()
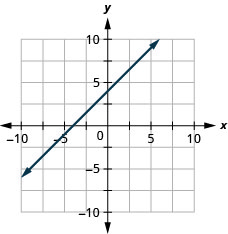
![]()
![]()
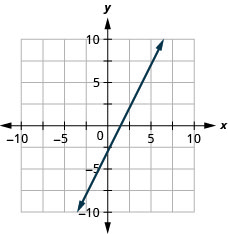
![]()
![]()
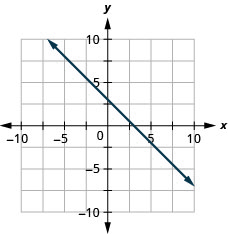
![]()
![]()
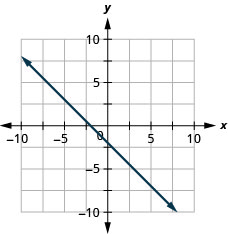
![]()
![]()
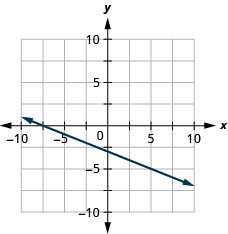
![]()
![]()
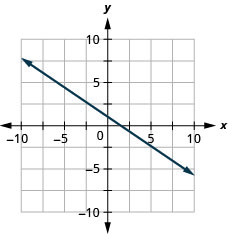
![]()
![]()
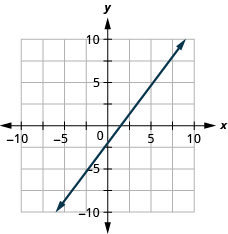
![]()
![]()
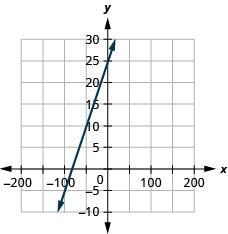
Cull the Most Convenient Method to Graph a Line
In the post-obit exercises, make up one's mind the most convenient method to graph each line.
![]()
![]()
horizontal line
![]()
![]()
vertical line
![]()
![]()
slope–intercept
![]()
![]()
intercepts
![]()
![]()
gradient–intercept
![]()
![]()
horizontal line
![]()
![]()
intercepts
![]()
![]()
slope–intercept
Graph and Interpret Applications of Slope–Intercept
The equation ![]() models the relation between the amount of Tuyet'due south monthly water bill payment, P, in dollars, and the number of units of water, w, used.
models the relation between the amount of Tuyet'due south monthly water bill payment, P, in dollars, and the number of units of water, w, used.
- ⓐ Find Tuyet'south payment for a month when 0 units of h2o are used.
- ⓑ Find Tuyet's payment for a month when 12 units of water are used.
- ⓒ Interpret the slope and P-intercept of the equation.
- ⓓ Graph the equation.
The equation ![]() models the relation between the amount of Randy's monthly h2o pecker payment, P, in dollars, and the number of units of water, w, used.
models the relation between the amount of Randy's monthly h2o pecker payment, P, in dollars, and the number of units of water, w, used.
- ⓐ Find the payment for a month when Randy used 0 units of water.
- ⓑ Discover the payment for a month when Randy used 15 units of water.
- ⓒ Interpret the slope and P-intercept of the equation.
- ⓓ Graph the equation.
- ⓐ ?28
- ⓑ ?66.10
- ⓒ The slope, 2.54, means that Randy's payment, P, increases past ?2.54 when the number of units of h2o he used, west, increases past 1. The P–intercept ways that if the number units of h2o Randy used was 0, the payment would be ?28.
- ⓓ
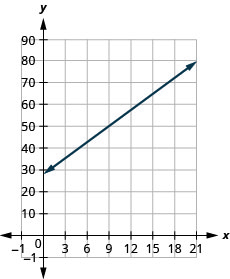
Bruce drives his machine for his job. The equation ![]() models the relation between the amount in dollars, R, that he is reimbursed and the number of miles, m, he drives in ane twenty-four hours.
models the relation between the amount in dollars, R, that he is reimbursed and the number of miles, m, he drives in ane twenty-four hours.
- ⓐ Find the corporeality Bruce is reimbursed on a day when he drives 0 miles.
- ⓑ Find the amount Bruce is reimbursed on a day when he drives 220 miles.
- ⓒ Interpret the gradient and R-intercept of the equation.
- ⓓ Graph the equation.
Janelle is planning to hire a car while on vacation. The equation ![]() models the relation between the toll in dollars, C, per twenty-four hours and the number of miles, m, she drives in one day.
models the relation between the toll in dollars, C, per twenty-four hours and the number of miles, m, she drives in one day.
- ⓐ Find the toll if Janelle drives the auto 0 miles i day.
- ⓑ Find the toll on a mean solar day when Janelle drives the car 400 miles.
- ⓒ Interpret the slope and C–intercept of the equation.
- ⓓ Graph the equation.
- ⓐ ?15
- ⓑ ?143
- ⓒ The gradient, 0.32, ways that the cost, C, increases by ?0.32 when the number of miles driven, yard, increases past ane. The C-intercept means that if Janelle drives 0 miles one twenty-four hours, the cost would be ?xv.
- ⓓ
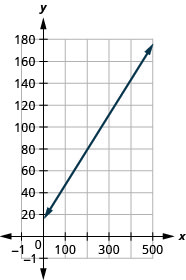
Cherie works in retail and her weekly salary includes commission for the corporeality she sells. The equation ![]() models the relation betwixt her weekly bacon, South, in dollars and the corporeality of her sales, c, in dollars.
models the relation betwixt her weekly bacon, South, in dollars and the corporeality of her sales, c, in dollars.
- ⓐ Find Cherie's salary for a calendar week when her sales were 0.
- ⓑ Observe Cherie's salary for a week when her sales were 3600.
- ⓒ Translate the gradient and Southward–intercept of the equation.
- ⓓ Graph the equation.
Patel'due south weekly salary includes a base of operations pay plus commission on his sales. The equation ![]() models the relation betwixt his weekly salary, S, in dollars and the amount of his sales, c, in dollars.
models the relation betwixt his weekly salary, S, in dollars and the amount of his sales, c, in dollars.
- ⓐ Find Patel's salary for a calendar week when his sales were 0.
- ⓑ Find Patel'south salary for a week when his sales were eighteen,540.
- ⓒ Interpret the slope and S-intercept of the equation.
- ⓓ Graph the equation.
- ⓐ ?750
- ⓑ ?2418.threescore
- ⓒ The gradient, 0.09, means that Patel's bacon, S, increases by ?0.09 for every ?i increase in his sales. The S-intercept ways that when his sales are ?0, his salary is ?750.
- ⓓ
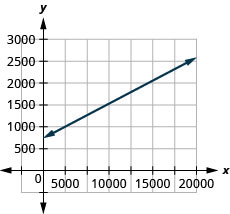
Costa is planning a dejeuner feast. The equation ![]() models the relation between the cost in dollars, C, of the banquet and the number of guests, g.
models the relation between the cost in dollars, C, of the banquet and the number of guests, g.
- ⓐ Find the cost if the number of guests is twoscore.
- ⓑ Detect the cost if the number of guests is 80.
- ⓒ Interpret the slope and C-intercept of the equation.
- ⓓ Graph the equation.
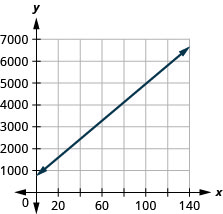
Margie is planning a dinner banquet. The equation ![]() models the relation betwixt the cost in dollars, C of the banquet and the number of guests, g.
models the relation betwixt the cost in dollars, C of the banquet and the number of guests, g.
- ⓐ Notice the cost if the number of guests is 50.
- ⓑ Detect the cost if the number of guests is 100.
- ⓒ Interpret the slope and C–intercept of the equation.
- ⓓ Graph the equation.
- ⓐ ?2850
- ⓑ ?4950
- ⓒ The slope, 42, means that the toll, C, increases past ?42 for when the number of guests increases past one. The C-intercept means that when the number of guests is 0, the cost would be ?750.
- ⓓ
Use Slopes to Identify Parallel Lines
In the post-obit exercises, apply slopes and y-intercepts to determine if the lines are parallel.
![]()
![]()
parallel
![]()
![]()
parallel
![]()
![]()
not parallel
![]()
![]()
parallel
![]()
![]()
parallel
![]()
![]()
parallel
![]()
![]()
parallel
![]()
![]()
parallel
![]()
![]()
non parallel
![]()
![]()
not parallel
![]()
![]()
not parallel
![]()
![]()
non parallel
![]()
![]()
non parallel
Apply Slopes to Place Perpendicular Lines
In the post-obit exercises, utilize slopes and y-intercepts to determine if the lines are perpendicular.
![]()
![]()
perpendicular
![]()
![]()
perpendicular
![]()
![]()
not perpendicular
![]()
![]()
not perpendicular
![]()
![]()
perpendicular
![]()
![]()
perpendicular
Everyday Math
The equation ![]() tin can be used to catechumen temperatures F, on the Fahrenheit calibration to temperatures, C, on the Celsius calibration.
tin can be used to catechumen temperatures F, on the Fahrenheit calibration to temperatures, C, on the Celsius calibration.
- ⓐ Explicate what the slope of the equation means.
- ⓑ Explicate what the C–intercept of the equation means.
The equation ![]() is used to guess the number of cricket chirps, north, in one minute based on the temperature in degrees Fahrenheit, T.
is used to guess the number of cricket chirps, north, in one minute based on the temperature in degrees Fahrenheit, T.
- ⓐ Explain what the gradient of the equation means.
- ⓑ Explain what the north–intercept of the equation means. Is this a realistic situation?
Writing Exercises
Explain in your own words how to decide which method to use to graph a line.
Why are all horizontal lines parallel?
Answers will vary.
Self Cheque
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After looking at the checklist, exercise you think you are well-prepared for the next section? Why or why non?
robbinsthornested.blogspot.com
Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/use-the-slope-intercept-form-of-an-equation-of-a-line/
Post a Comment for "What is the slope of a line that is perpendicular to y = 1/8x- 9?"